The equation of the curve passing through the origin and satisfying the differential equation (1x 2) dxdy 2xy=4x 2 is Medium View solution > Solve ( y 3 x 2) d y d x = x Medium View solution > The solution of the equation (xy) dy (xy) dx =0 isSolution for X^24y^24xy1=0 equation Simplifying X 2 4y 2 4xy 1 = 0 Reorder the terms 1 X 2 4xy 4y 2 = 0 Solving 1 X 2 4xy 4y 2 = 0 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '1' to each side of the equation 1 X 2 4xy 1 4y 2 = 0 1 Reorder the terms 1 1 X 2 4xy 4y 2 = 0 1 CombineIdentical expressions (x^ two)y' (x^ two)(y^ two) four xy 4= zero (x squared )y stroke first (1st) order plus (x squared )(y squared ) minus 4xy plus 4 equally 0

Separate Equations Of Lines Auxiliary Equation Method The Fact Factor
(x y)^2-4xy formula
(x y)^2-4xy formula-Answer (1 of 2) > > x = y cosec^2x = 4xy(xy)^2 4xy = (xy)^2 (xy)^2 So , Our Equation can be written as => cosec^2x = ((xy)^2 (xy)^2)/(xy)^2 =>cosec^2x = 1Degree 2 the quadratic polynomials x2−y2 and xyare harmonic;




Tinkutara Equation Editor Math Forum Question
Solution for X^24xyy^2=0 equation Simplifying X 2 4xy y 2 = 0 Solving X 2 4xy y 2 = 0 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '4xy' to each side of the equation y = arctan(x)/(1x^2)^2 C/(1x^2)^2 We have (1x^2)y'4xy=(1x^2)^2 A We can rearrange A as follows (1x^2)y'4xy = 1/(1x^2)^2 dy/dx (4x)/(1x^2)y = 1/(1x^2)^3 B We can use an integrating factor when we have a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;1 4x2y p x y = 4xy2 x y 1 dy dx = (4xy2 p x y) 1 1 4x2y p x y 7Find all the xcoordinates of the points on the curve x2y2 xy= 2 where the slope of the tangent line is 1 We need to nd the derivative dy dx by implicit di erentiation Di erentiating with respect to xon both sides of the equation, 2xy2 x2 2y dy dx y x dy dx = 0 Here
This differential equation is called an Euler differential equation We seek solutions of the form y(x) = xr y ( x) = x r Substituting yields an algebraic equation for r r of the form a2r(r−10 0 View solution steps Solution Steps 2xy (5x (3x)) (2x (4xy2xy)) 2 x y − ( 5 x − ( 3 x)) − ( − 2 x − ( − 4 x y 2 x y)) Combine 5x and 3x to get 2x Combine 5 x and − 3 x to get 2 xThe new equation is exact since M y = N x = 4xy 2x Now integrate Mand N Z M(x;y)dx= Z (2xy 2 2xy 4x3)dx= xy2 x2y x4 g(y);
Answer (1 of 7) There are many method or ways to solve this question METHOD1 so if know the formula (XY) ^2=(XY) ^2 4XY Substituting the values We get 11^2=(XY) ^2 23 121 23 = (XY) ^2 144 = (XY) ^2 Therefore (XY) = 12 METHOD 2 IfCombine 2xy and 4xy to get 2xy x^ {2}\left (2y\right)xy^ {2}=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction Consider the system of linear equations in x, y, z (sin 3θ) x y z = 0 (cos 2θ) x 4y 3z = 0 asked in Mathematics by Amita ( 5k points) trigonometrical equations




Cauchy Riemann Show That U V X Y X2 4xy Y2 Find F Z Youtube




Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf
Solve the differential equation (x^2 6y^2) dx 4xy dy = 0 when x= 1 y= 1 using at least three methods Question Solve the differential equation (x^2 6y^2) dx 4xy dy = 0 when x= 1 y= 1 using at least three methodsSec 2 θ = 4xy/(x y) 2 is true if and only if 1) x y ≠ 0 2) x = y, x ≠ 0 3) x = y 4) x ≠ 0, y ≠ 0 Answer (2) x = y, x ≠ 0 Solution Given, sec 2 θ = 4xy/(x y) 2 We know that, sec 2 θ ≥ 1 Therefore, 4xy/(x y)2 ≥ 1Q The equation $14x^2 4xy 11y^2 = 60$ represents a certain locus If the axes are rotated through an angle $\tan^{1} \, 2$, without change of origin then the equation of the locus referred to new axes becomes




In Order To Eliminate The First Degree Terms From The Equation 2x 2 4xy 5y 2 4x 22y 7 0 The Point To Which Origin Is To Be Shifted Is




Answered 9x 24xy 16y 100 X Y 1 Bartleby
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Show that the equation `sec^2 theta=(4xy)/(xy)^2` is only possible when x=ySolve (x^2 1)y" 4xy' 2y = 2/x 1 such that the general solution obeys the initial conditions y (0) = 1 and y' (0) = 5 and given that y_1 = 1/x 1 and y_2 = 1/x 1 are solutions to the homogeneous version As a check to our sanity we should try to do the same problem in two different ways to make sure everything is working correctlyPlease be sure to answer the questionProvide details and share your research!




Factorise X Y 2 4xy Z 2 Brainly In



If Xy 2 12 And Xy 4 What Does X Equal Quora
X^2*y x^2 y' = 0;Example 1 Determine the critical points and locate any relative minima, maxima and saddle points of function f defined by f(x , y) = 2x 2 2xy 2y 2 6x Solution to Example 1 Find the first partial derivatives f x and f y f x (x,y) = 4x 2y 6 f y (x,y) = 2x 4y The critical points satisfy the equations f x (x,y) = 0 and f y (x,y) = 0 simultaneously HenceIf negative, an ellipse;
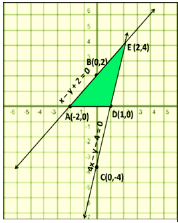



Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 And 4x Y 4 0 Calculate The Area Of The Triangle Formed By The Lines So Drawn And The X Axis Snapsolve




Solved 1 Find And Sketch The Domain Of The Following Chegg Com
(a) the new formula fo rq=x 2 y2 (b) the old formula fo rq=XY (c) the equation of the circle x 2 y2 = 1 in the new system 9 In the usual x,y coord system, q is 2x 2 3xy4y2 Switch to a new X,Y coord system which has the same axes as before but new scales If the old scale was the inch, on the new Xaxis use the foot and on the new YaxisCalculus Find dy/dx x^24xyy^2=4 x2 4xy y2 = 4 x 2 − 4 x y y 2 = 4 Differentiate both sides of the equation d dx (x2 4xy y2) = d dx(4) d d x ( x 2 − 4 x y y 2) = d d x ( 4) Differentiate the left side of the equation Tap for more stepsEquation at the end of step 1 Step 2 Equation at the end of step 2 Step 3 x 2 3xy 10y 2 Simplify ——————————————— x 2 4xy 5y 2 Trying to factor a multi variable polynomial 31 Factoring x 2 3xy 10y 2 Try to factor this



What Is The Formula Of X Y 2 Quora




Distance Between The Two Lines Represented By The Line Pair X 2 4xy 4y 2 X 2y 6 0 Is
Now we can replace the g(x) in equation 2 in equation 1 I(x, y) = 2y 3 − x 2 y 3y x 3 2x C And the general solution is of the form I(x, y) = C and so (remembering that the previous two "C"s are different constants that can be rolled into one by using C=C 1 C 2) we getPolynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2 Example 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2Suppose the curves are x = y2 and x = 4 y2 and and you want to find points on the two curves with the same yvalue Then substitute y 2 from the first equation into the second to obtain x = 4 x So to achieve the same yvalue the xvalue on the second curve must be (minus) 4 times the xvalue on the first curve x = 4y2 and x = y2



How Do You Graph The Conic X 2 4xy Y 2 1 0 By First Rotations The Axis And Eliminating The Xy Term Socratic




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com
But avoid Asking for help, clarification, or responding to other answersAnswer x^24y^2=4xy x^24y^24xy=0 Using the formula (ab)^2=a^2b^22ab here a=x,b=2y so, (x2y)^2=0 x2y=0 x=2y x/y=2/1Section 145 (3/23/08) Directional derivatives and gradient vectors Overview The partial derivatives fx(x0,y0) and fy(x0,y0) are the rates of change of z = f(x,y) at (x0,y0) in the positive x and ydirectionsRates of change in other directions are given by directional



The Area Bounded By The Circles X2 Y2 1 And X2 Class 10 Maths Cbse



X2 Y2 2 4xy Find Dy Dx Mathematics Topperlearning Com 6729
Click here👆to get an answer to your question ️ The equation x y = 4 and x^2 4xy y^2 = 0 represent the sides of Section 43 Double Integrals over General Regions In the previous section we looked at double integrals over rectangular regions The problem with this is that most of the regions are not rectangular so we need to now look at the following double integral, ∬ D f (x,y) dA ∬ D f ( x, y) d A where D D is any region 1 The value of cos236° cos254° is 2 If sinθcosθ s i n θ c o s θ = p and secθcosecθ s e c θ c o s e c θ = q , then the value of q(p2 −1) q ( p 2 − 1) is 3 From the top of a lighthouse at a height metres above sealevel, the angle of depression of a ship is 300 30 0 The distance of the ship from the foot of the




Show That The Lines X 2 4xy Y 2 0 And X Y 4 Form An Equilateral Triangle Also Find The Area Of The Triangle




Conic Section From Expanded Equation Ellipse Video Khan Academy
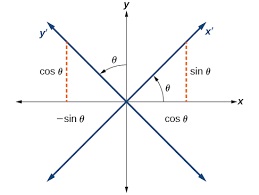
Please see below A conic equation of the type of Ax^2BxyCy^2DxEyF=0 is rotated by an angle theta, to form a new Cartesian plane with coordinates (x',y'), if theta is appropriately chosen, we can have a new equation without term xy ie of standard form The relation between coordinates (x,y) and (x'y') can be expressed as x=x'costhetay'sintheta and Simplify Do not use negative exponents in the answer 12x2y4 3xy7 There should be a line between like a fraction but it did not copy or paste This is the answer I got 12 x^2 y^4 = 12y^4/x^2 3xy^7 = 3x/y^7 it was wrongFind the separate equation of the line represented by the following equation x 2 4xy = 0 Advertisement Remove all ads Solution Show Solution x 2 4xy = 0 ∴ x (x 4y) = 0 ∴ the separate equations of the lines are x = 0 and x 4y = 0 Concept Combined Equation of a



1




If Cosec 2 Theta 4xy X Y 2 Then Find The Relation Between X And Y Mathematics Topperlearning Com R0vcgjee
Learn to factorise an expression of the form x^4 x^2y^2 y^4 This is solved by adding and subtracting x^2y^2 to the given expression and reducing it to t3 ( x y) 2 − ( x − y) 2 = 2 This is the equation of a herperbola There's a quick way of making a qualitative determination ignore the terms of degree less than 2, to get something that looks like A x 2 B x y C y 2 Then look at the discriminant, B 2 − 4 A C If positive, you have a hyperbola;Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor




Factorise X Y 2 4xy Z 2 Brainly In




Example 21 Factorize 4x2 Y2 Z2 4xy 2yz 4xz Examples
Dy/dx P(x)y=Q(x) So we form an Integrating Factor;Given 5x 2 4xy 5y 2 = 110 and the point (5, 3) To be able to find the equation of the tangent line to ellipse, we first of all need to determine the slope or gradient by differentiating the ellipse functions and then substituting the point (5, 3) into it We then use y y 1 = m(x x 1) to get the tangent line 5x 2 4xy 5y 2 = 110All other harmonic homogeneous quadratic polynomials are linear combinations of these φ(x,y) = a(x2 −y2)bxy, (a,bconstants) Degree n the real and imaginary parts of the complex polynomial (xiy)n are harmonic (Check this against the above when n= 2) B Functions with




Exact Equations Example 3 Video Khan Academy




Tinkutara Equation Editor Math Forum Question
what is the differential equation of (3x^22y^2)(14xy)dy/dx=0 1Solve the differential equation dy/dx= y^2/x^3 for y=f(x) with the condition y(1) = 1 2Solve the differential equation y prime equals the product of 2 times x and the square root of the quantity 1 minus y squared Explain why 🔴 Answer 3 🔴 on a question (xy)^2(xy)^2=4xy the answers to answerhelpercom M = x 2 4xy 2y 2, N = y 2 4xy 2x 2 dM/dy = 4x 4y dN/dx = 4y 4x Therefore, dM/dy = dN/dx So, the given differential equation is exact On integrating M wrt x, treating y as a constant, On integrating N wrt y, treating x as a constant, (omitting 2xy 2 2x 2 y which already occur in ∫M dx) Therefore, the solution of




Example 11 Find Particular Solution Dy Dx 4xy2 Examples



Doab Is Formed By The Lines X2 4xy Y2 0 And The Line Ab The Equation Of Line Ab Is 2x 3y 1 0 Find The
Solve the following system of equations 3x 4xy 2y = 2 3x 2y = 10 Solve the second equation for either of the unknowns I'll pick x 3x 2y = 10 add 2y to both sides 3x = 10 2y Divide both sides by 3 x = (10 2y)/3 factor out 2 x = 2 (5 y)/3 In the first original equation, 3x 4xy Thanks for contributing an answer to Mathematics Stack Exchange!We have to solve the simultaneous equation y^2 4xy 4y = 1 (1) 3x^2 2xy = 1 (2) We see that it is not possible to isolate x in terms of y or y in terms of x using any of the equations



Sec 28 4xy X Y 2 Is True If Any Only If Sarthaks Econnect Largest Online Education Community




Answered Find The Angle Of Rotation And Bartleby
The equation xy=4 and x^24xyy^2=0 represent the sides of This browser does not support the video element Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams Angle bisectors of , so the given triangle is equilateral triangleZ N(x;y)dy= Z (2x2y x2)dy= x2y2 x2y h(x) Therefore, an implicit solution is x 2y x2y x4 = C Homework p 67, #113 oddSeparabledifferentialequationcalculator y'4xy^{2}=x en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Separable ODE Last post, we talked about linear first order differential equations In this post, we will talk about separable



Secure Media Collegeboard Org




Deltaoab Is Formed By The Lines X 2 4xy Y 2 0 And The Line Ab The Equation Of Line Ab Is 2x 3y 1 0 Find The Equation Of The Median Of The Triangle
Engineering in your pocket Now study onthego Find useful content for your engineering study here Questions, answers, tags All in one app!You can put this solution on YOUR website!Joint equation of pair of lines through (3, 2) and parallel to x 2 4xy 3y 2 = 0 is Joint equation of pair of lines through (3, 2) and parallel to x 2 4xy 3y 2 = 0 is 1) x2 3y2 – 4xy – 14x 24y 45 = 0 2) x2 3y2 4xy 14x 24y 45 = 0 3) x2 3y2 4xy – 14x 24y – 45 = 0




If 5x 2 4xy Y 2 2x 1 0 Then X Y




Mathematics Cartesian Coordinate Geometry And Straight Lines Session Ppt Download




Mathematics Class 9th Chapter 4 Solution
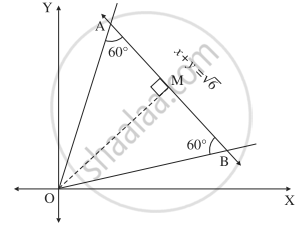



Show That The Lines X2 4xy Y2 0 And The Line X Y 6 Form An Equilateral Triangle Find Its Area And Perimeter Mathematics And Statistics Shaalaa Com



Identifying Conics By The Discriminant




Solved Question 5 13 Pts Write The Appropriate Rotation Chegg Com




5023 Max Min Optimization Ap Calculus Open Intervals




Factorize 1 X 2 1 Y 2 4xy Brainly In




Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy



Linear Differential Equations As A Data Structure Springerlink



Solved Compute The Second Partial Derivatives 2 F X 2 2 F X Y 2 F Y X 2 F Y 2 For The Following Function F X Y 2 Xy X 2 Y 2 Course Hero




Example 11 Find Particular Solution Dy Dx 4xy2 Examples
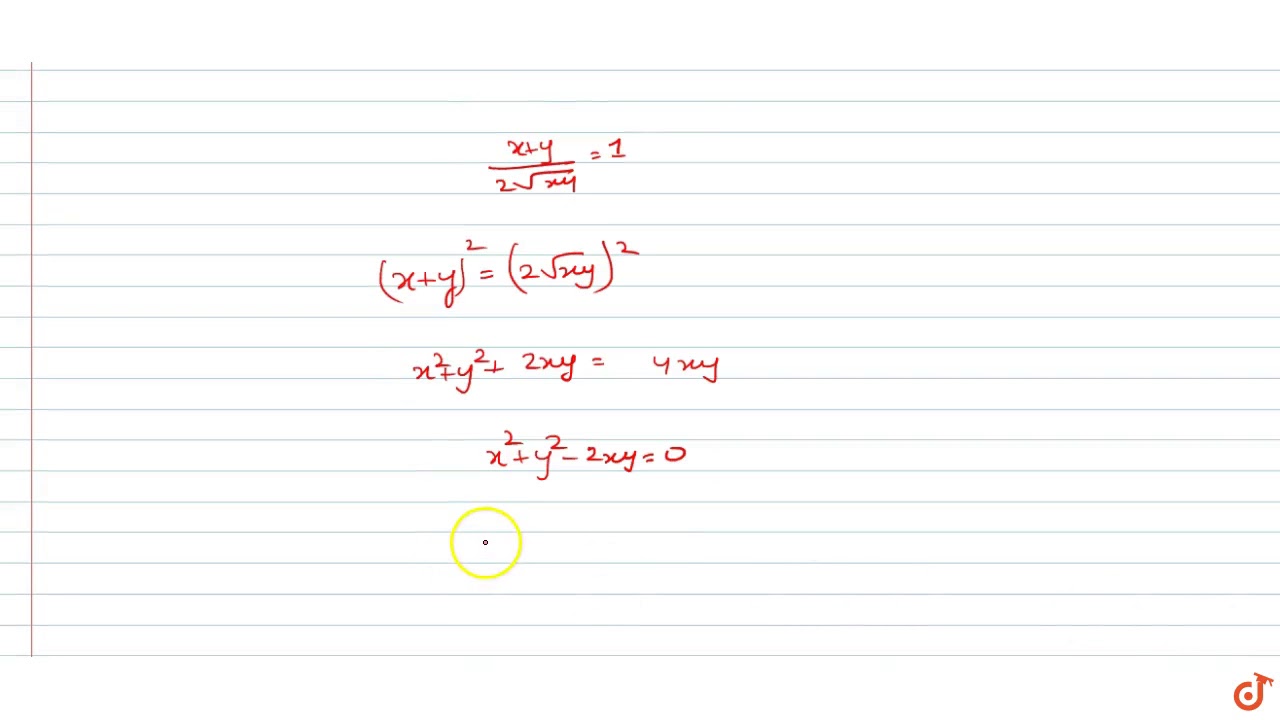



If Sec 2 Theta 4xy X Y 2 Then How Many Pairs Of X And Y Are There For Which The Condition Youtube



Factorize X Y 2 4xy




25 Factorise X Y 2 4xy 9z 2 2392 Mbaheblogjp5ypl




Find The Minimum Value Of X 2 4xy 4y 2 2z 2 Given That Xyz 32 Mathematics Stack Exchange




X 2 Y 2 0 Represents Huscleod




Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Amp 4x Y 4 0 Determine The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines



Factorise 1 X 2 1 Y 2 4xy Scholr




View Question Rotate The Axes




Selina Chapter 4 Expansions Including Substitution Icse Solutions Class 9 Maths




What Is The Value Of X 4xy Y Over 2xy X Y Youtube




Show That The Equation Sec 2 Theta 4xy X Y 2 Is Only Possible When X Y




Sec 2theta 4xy X Y 2 Is True If And Only If




Calc 501 1000 By James Bardo Issuu



Secure Media Collegeboard Org




If X2 Y2 2 Xy Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Gwvwfskk




Inequality Of Arithmetic And Geometric Means Wikipedia




Recitation 4 24xy For 0 X 1 0 Y 1 X Y 1 0 Elsewhere Pdf Free Download



Solved Write The Equations Of The Lines I Parallel Ii Perpendicular To The Given Line Passing Through The Point P A P 1 Aˆ 2 2x Aˆ Y 4 B P Aˆ 1 0 Y Aˆs5




Separate Equations Of Lines Auxiliary Equation Method The Fact Factor



Secure Media Collegeboard Org




Darlene Wrote This Proof Of The Identity X Y 2 X Y 2 4xy Which Of The Following Is A Justification For Step 5 Of



Secure Media Collegeboard Org



The Equation X Y 4 And X 2 4xy Y 2 0 Represent The Sides Of Youtube




Useful Algebra Formulas For Competitive Exams Pdf




Factorise The Following Expression X Y 2 4xy Brainly In
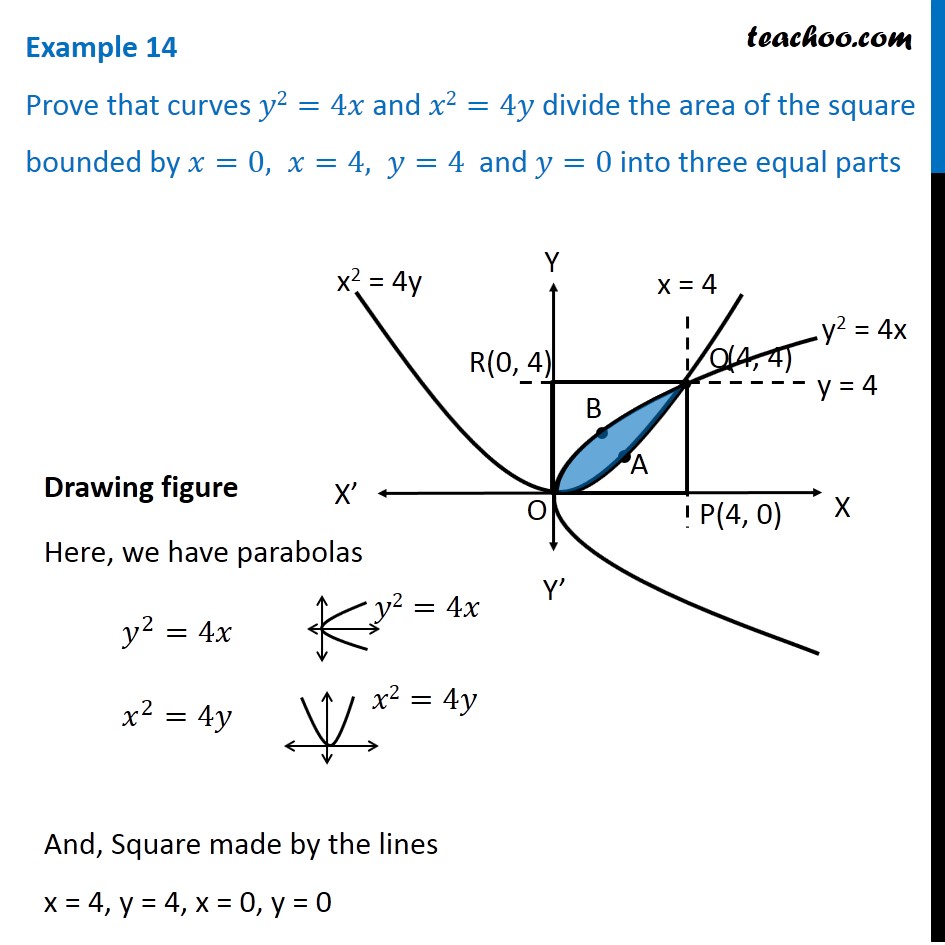



Example 14 Prove That Y2 4x X2 4y Divide Area Of Square




Algebraic Expressions Class 7 Extra Questions Maths Chapter 12 Learn Cbse



X2 6x 16



The Line X 2 4xy Y 2 0 And X Y 4 Are The Sides Of An Equilateral Triangles Whose Area Is Equal To A 3 1 2 Then A Is Equal To Sarthaks Econnect Largest Online Education Community




25 Factorise X Y 2 4xy 9z 2 2392 Mbaheblogjp5ypl




Show That The Lines X 2 4xy Y 2 0 And X Y 1 Form An Equilateral Triangle And Find Its Area




Solved No For The Equation 4x Y Xy 1 X Y 0 We Look Chegg Com




Solved 1 Find Oz X Xy B Z 4xy D In Xy 2 Use Chegg Com




Solved Write The Appropriate Rotation Formulas So That In A Chegg Com




Example Algebraic Vector Photo Free Trial Bigstock




Today S Class Derivatives Of Multivariate Functions Ppt Download



1




Solved Find All Second Order Partial Derivatives For The Chegg Com



The Line X 2 4xy Y 2 0 And X Y 4 Are The Sides Of An Equilateral Triangles Whose Area Is Equal To A 3 1 2 Then A Is Equal To Sarthaks Econnect Largest Online Education Community
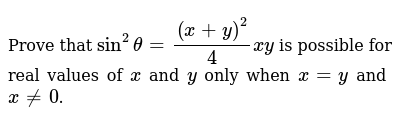



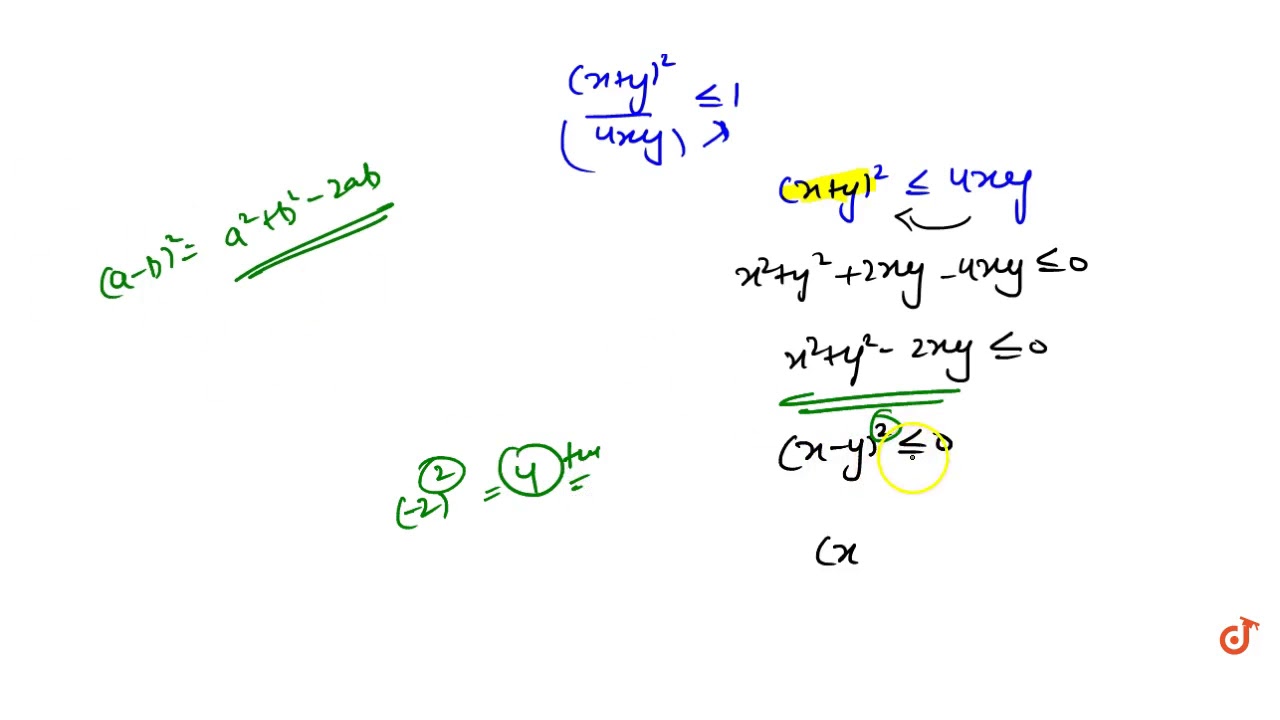
Prove That Sin 2theta X Y 2 4xy Is Possible For Real Values Of X And Y Only When X Y And X 0



Sin 2 Theta X Y 2 4xy Where X Y In R Gives Theta If And Only If Youtube




Solutions To Implicit Differentiation Problems




Find All Points Of Intersection Of The Graphs Of X 2 4x Y 5 And X Y 9 Study Com




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf



How To Factorize X Y Y X Quora




Prove That Sin 2theta X Y 2 4xy Is Possible For Real Values Of X And Y Only When X Y And X 0
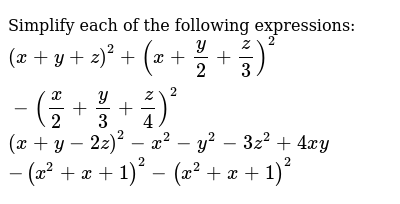



Simplify X Y 2z X Y 3z 4xy
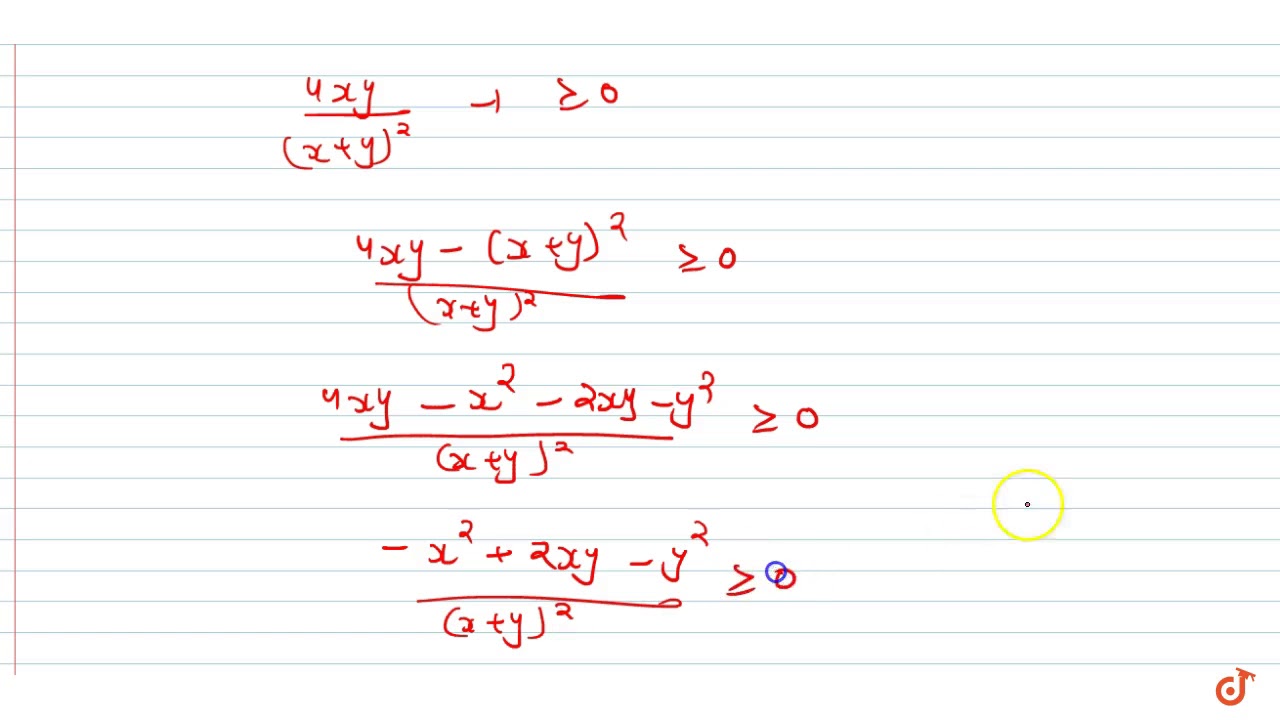



Show That The Equation Sec 2 Theta 4xy X Y 2 Is Only Possible When X Y Youtube
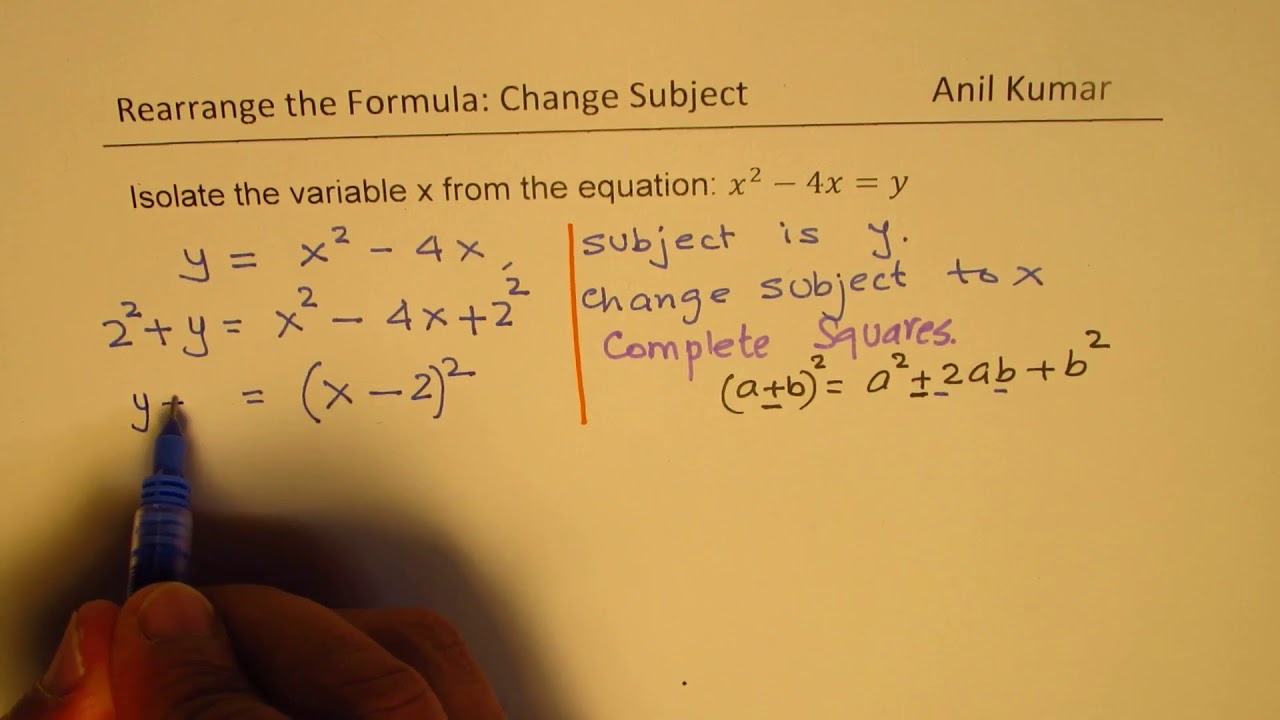



Completing Squares To Rearrange Formula X 2 4x Y Changing Subject Youtube
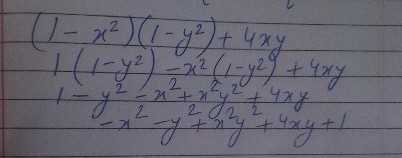



Factorise 1 X 2 1 Y 2 4xy Scholr



Geometry Formulas
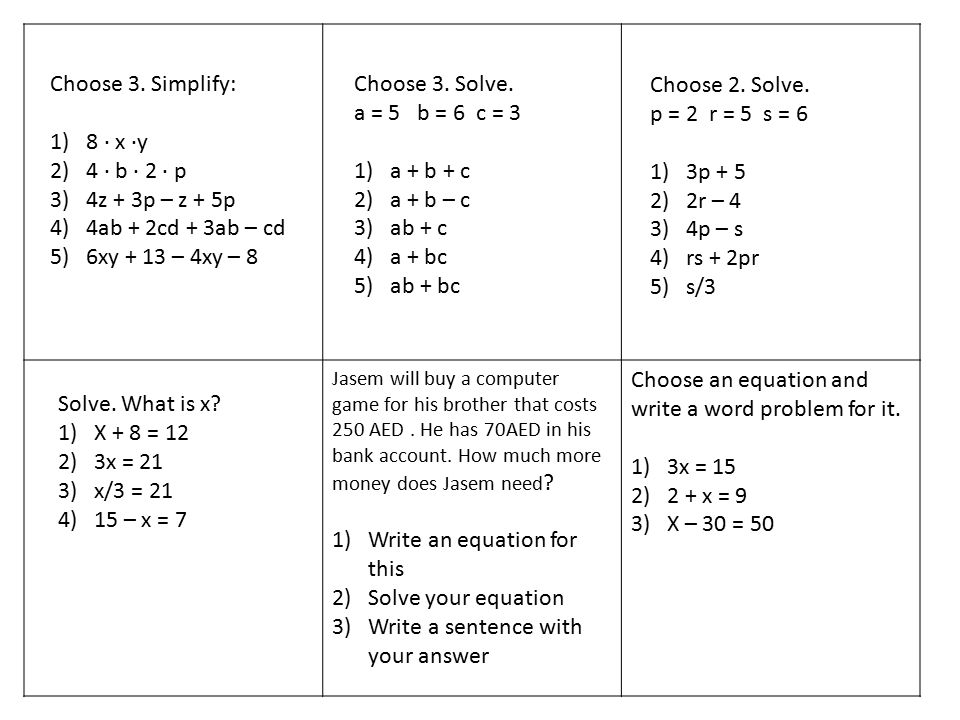



Jasem Will Buy A Computer Game For His Brother That Costs 250 Aed He Has 70aed In His Bank Account How Much More Money Does Jasem Need 1 Write An Equation Ppt Download




Name Fased Al Hamvn Own Ee1 Quiz4 Solve The Equations p 23 Solutions Xy 2 4x 3y 11 2x Y Homeworklib




If Cosec 2 Theta 4xy X Y 2 Then Find The Relation Between X And Y Brainly In



Www3 Nd Edu




How To Solve Exact Differential Equations In Matlab Stack Overflow




Solution Sqrt Studypool
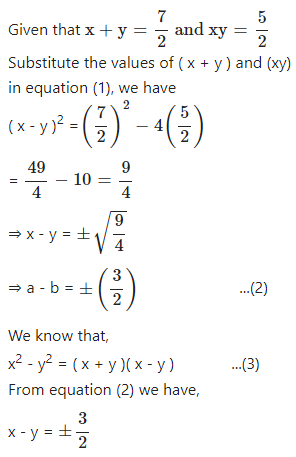



Expansions Icse Class 9th Concise Selina Mathematics Icsehelp




3 Systems Of Linear Equations




Find The Angle Through Which The Axes Are To Be Rotated So As To Remove The Xy Terms In Equation X2 Brainly In
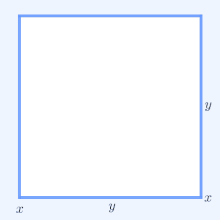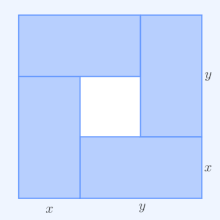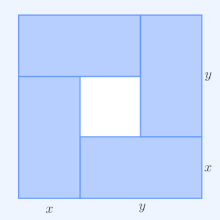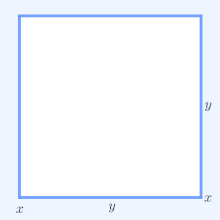



Inequality Of Arithmetic And Geometric Means Wikipedia



If X Y 2 Then What Is The Value Of X Y 6xy Quora



Jstor Org




Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy



0 件のコメント:
コメントを投稿