Answer to Solve the initialvalue problem y' 4xy = x^3 e^{x^2}, y(0) = 8 By signing up, you'll get thousands of stepbystep solutions to for Teachers for Schools for Working Scholars® forQuestion Solve the linear ODE y' 4xy = x^3 e^x^2 This problem has been solved!Consider x^ {2}y^ {2}xy22xy as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factor

Solucionarioecuacionesdiferencialesdenniszill7aedicion P
Y'+4xy=x^3e^x^2
Y'+4xy=x^3e^x^2- y'=(3 e^y*cos (3xy)4xy y^2)/(2xy2x^2e^y*sin (3xy)e^y*cos(3xy)) From the given 1=x y^22x^2 y e^y*sin (3xy) Differentiate both sides of the equation with respect to x it goes like this d/dx(1)=d/dx(x y^2)d/dx(2 x^2 y)d/dx(e^y* sin (3xy)) 0=x*2y y'y^2*12x^2 y'y*2xe^y*y'*sin(3xy)e^y*cos(3xy)*(3y') simplification, it follows 0=2xyy'y^22x^2y'4xye^y sin(3xy)y'3 e^y cos(3xy)e^y cos(3xy)y' collecting terms with y Transcript Example 21 Factorize 4x2 y2 z2 – 4xy – 2yz 4xz 4x2 y2 z2 – 4xy – 2yz 4xz = 22 x2 y2 z2 – 4xy – 2yz 4xz = (2x)2 y2 z2



2
4 y 2 d x 2 − 3 d x 4 d y = 0 Combine all terms containing d Combine all terms containing d \left (4y^ {2}x^ {2}3x4y\right)d=0 ( 4 y 2 x 2 − 3 x 4 y) d = 0 The equation is in standard form The equation is in standard form \left (4x^ {2}y^ {2}3x4y\right)d=0 ( 4 x 2 y 2 − 3 x 4 y) d = 0Y=xex Kex To get y(1 )=3need3=eKe,K= 3e e Answer is y = xe x 3e e e x =xex 3ex1 ex method 2 (since coeffs are constant) m = 1, y h =Aex Try y p = Bxe x (step up) NeedBxe x Bex Bxe x =ex xe x terms drop out Equate coeffs of the e x terms B = 1 Gen sol is y = Ae x xex The IC determine A as in method 1 6I = e^(int P(x) dx) \ \ = exp(int \ 4x \ dx) \ \ = exp( 2x^2 ) \ \ = e^(2x^2
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicSolve the linear ODE y' 4xy = x^3 e^x^2;Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is
Math 217 Midterm 2 13Each of the choices presents three functions y 1;y 2;The function y1=x^2 is a solution of x^2y''3xy'4y=0 find the general differential equation by reducing its order Show all work 1 y= Cx^2Dx lnx 2 y=Cx^2D ln/x 3 y=Cx^2Dx^2 lnx 4 y=Cx^2Dx^2 sinx 5 None of the above These are the optionsAnd y 3, which are solutions to a thirdorder homogeneous linear equation of the form y(3) p 1(x)y00 p 2(x)y0 p 3(x)y = 0;



How To Solve The Differential Equation D 3 Y Dx 3 D 2 Y Dx 2 3 Dy Dx 5y 5sin2x 10x 2 3x 7 Quora



1
X^2 y^2 x 4y 1/4 = 0, 2xy3=0 , 4xy=0 , y=0 Natural Language;Step 2 Equation at the end of step 2 (2x 2 • y) 2 2 xy 3 Step 3 Step 4 Pulling out like terms 41 Pull out like factors 2x 2 y 4xy 3 = 2xy • (x 2y 2) Trying to factor as a Difference of Squares 42 Factoring x 2y 2 Theory A difference of two perfect squares, A 2 B 24xy'' 2y' y = sin sqrt(x);
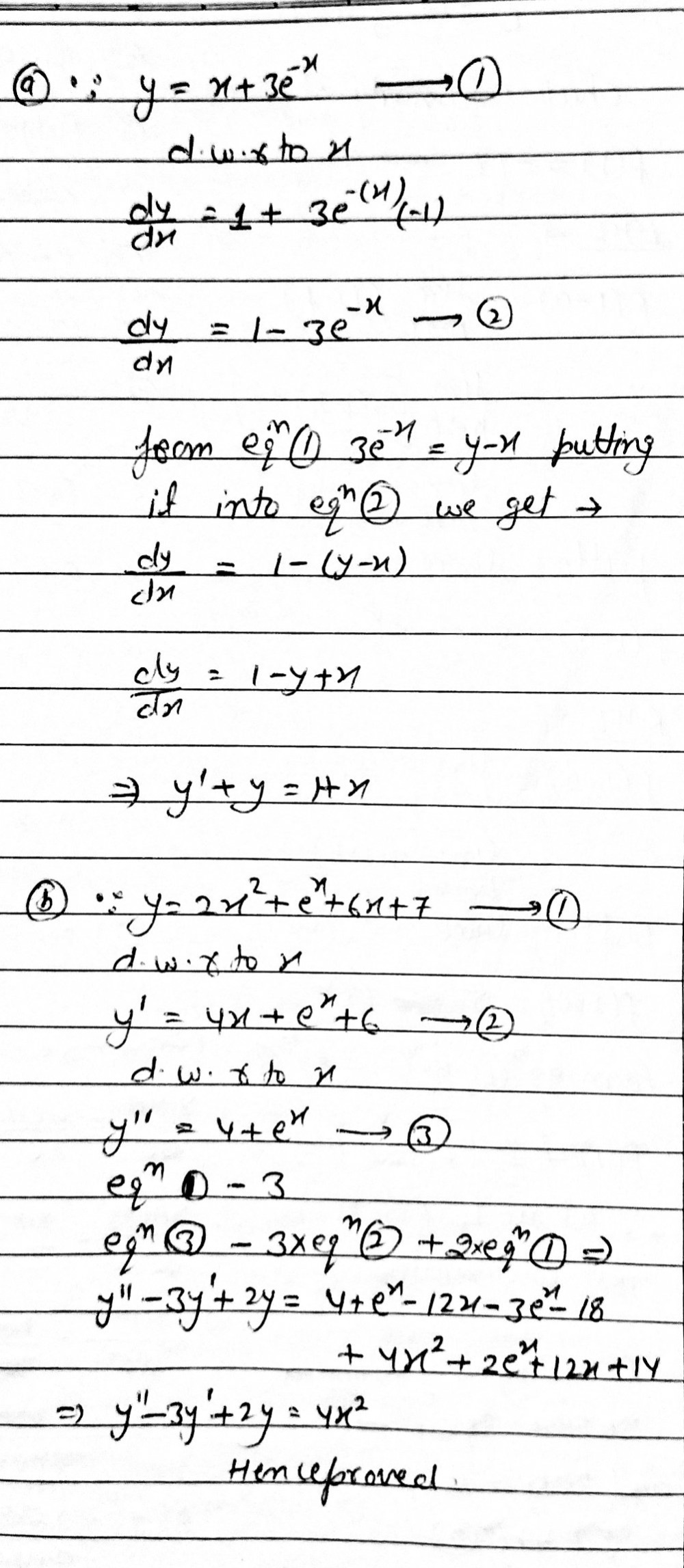



A Y X 3e X Mled Below Is Solution Of The Different Gauthmath
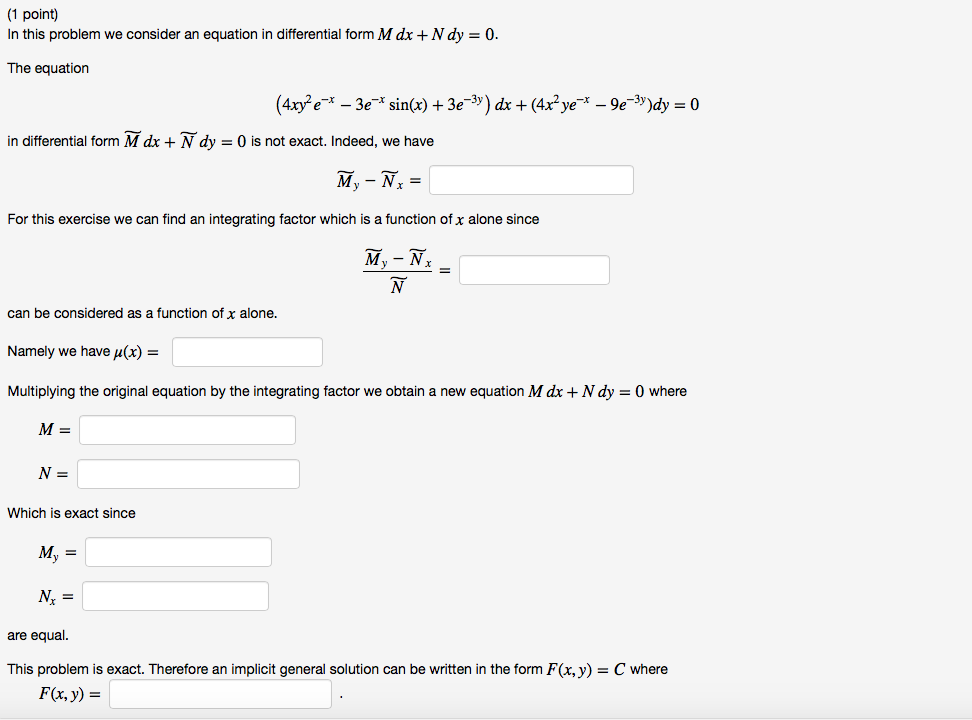



In This Problem We Consider An Equation In Chegg Com
WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range of people—spanning all professions and education levelsOnce again I have some crazy relationship between x and y and just to get a sense of what this might look like if you plot all the X's and Y's that satisfy this relationship you get this nice little clover pattern and I plotted this off of Wolfram Alpha but what I'm curious about in this video is you might imagine from the title is to figure out the rate at which Y is changing with respect toDefinition 2 Let X,Y be jointly continuous random variables with joint density fX,Y (x,y) and marginal densities fX(x), fY (y) We say they are independent if fX,Y (x,y) = fX(x)fY (y) If we know the joint density of X and Y, then we can use the definition to see if they are independent But the definition is often used in a different




Engineering Mathematics Notes




Cobalt Induced Synthesis Of 6 Pyridin 2 Yl Purines By Microwave Enhanced 2 2 2 Cyclotrimerization Turek 08 European Journal Of Organic Chemistry Wiley Online Library
73E Series Solutions Near an Ordinary Point I (Exercises) Last updated Find a power series in \(x\) for the general solution of \(1x^2)y''4xy'2y=0 \tag{A}\ Use (a) and the formula \{1\over1r}=1rr^2\cdotsr^n\cdots \quad(1Experts are tested by Chegg as specialists in their subject area We review their content andThat's a Riccati equation 1 First divide by x 2 y ′ = 4 7 x − 1 y 2 x − 2 y 2 Now let v = 2 x − 2 y We obtain v ′ = − 4 x − 3 y 2 x − 2 y ′, so that y ′ = 1 2 x 2 v ′ 2 x − 1 y Moreover, v 2 = 4 x − 4 y 2, so that y 2 = 1 4 x 4 v 2 Substituting these expressions in the differential equation, we get



Www Kirschhecke De Wp Content Uploads 04 Terme Und Gleichungen Pdf



Solve The Differential Equation Dy Dx 3e 2x 3e 4x E X E X Quora
24x => 24 => 24 => 0 (zero) $$ x^2 y'' 2 x y' 2y = x^4 \mathrm{e}^x $$ I tried to solve it but finally I stuck tell me how to go further more if anyone gives me Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and buildFactor out the Greatest Common Factor (GCF), '4xy' 4xy(y x) = 0 Ignore the factor 4 Subproblem 1 Set the factor 'xy' equal to zero and attempt to solve Simplifying xy = 0 Solving xy = 0 Move all terms containing x to the left, all other terms to the right




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Example 2 Verify That Y E 3x Is A Solution Of Y Y 6y 0
Yh(x) = c1e−x c2e3x is the general solution to the corresponding homogeneous differential equation As noted in corollary 2, it then follows that y(x) = yp(x) yh(x) = 3e5x c1e−x c2e3x is a general solution to our nonhomogeneous differential equationY1 = cos sqrt(x), y2 = sin sqrt(x) xy'' − (2x 2)y' (x 2)y = 6x^3e^x ;Y1 = x cos x, y2 = x sinx




1 Find The General Solutions X 2y 4xy 6y 0 Chegg Com




Paper
Dy/dx P(x)y=Q(x) The given equation is already in standard form, so the integrating factor is given by;Y = x^4 3x^2 10x 9?Solution for Let p(x, y) = x² 8y² 4xy 2x Calculate the following generalized integral, or show that it diverges, ep(x,y)dA R2



Www Math Ucla Edu Yanovsky Handbooks Pdes Pdf




2 Pdf Equations Elementary Mathematics
Simplify (4xy)/(x^2y^2)(xy)/(xy) Since both terms are perfect squares , factor using the difference of squares formula , where and To write as a fraction with aForcing y as a solution, cancelling e 2 x in both sides, and equalling the coefficients, we obtain { 4 a 2 b = 0 8 b 6 c = 0 12 c = 1 It is easy to check that a = 1 32, b = − 1 16 and c = 1 12 do the job With this, the general solution to the equation is y = ( c 1 x 32 − x 2 16 x 3 12) e 2 x c 2 e − 2 x, c 1, c 2 ∈ R Share y = (x43)e^(2x^2) We have y' 4xy = e^(2x^2) A We can use an integrating factor when we have a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;



Www Springer Com Cda Content Document Cda Downloaddocument Aufgaben Kap 8 Pdf Sgwid 0 0 45 P
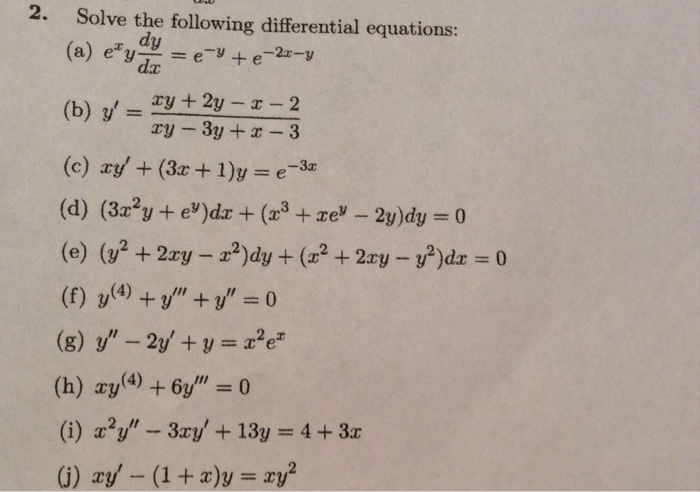



Solve The Following Differential Equation E Xy Dy Dx Chegg Com
Y1 = e^x , y2 = x^3e^x x^2y''− 2xy' (x^2 2)y = x^3 cos x;Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is aSimple and best practice solution for X^24xyy^2=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Chapter 19 Solutions Manual Calculus Iii Math 2401 Docsity
X^3 x^2 y x y^2 y^3 Natural Language; (x24xy2y2)dx(y24xy2x2)dy=0 calculus Find the critical point(s) of the function Then use the second derivative test to classify the nature of each point, if possible Finally, determine the relative extrema of the function f(x,y)= 3x^2 3e^5y^2 Derivative Test Consider the function y = 3x5 – 25x3 60x 12 x2ex 11 y00 y0 1 4 y = 3 e 1 2 x Sol The characteristic equation m2 m 1 4 = (m 1 2) 2 = 0 has a root m = 1 2 with multiplicity 2 The complementary solution is y c = C 1e 1 2 x C 2xe 1 2 x In view of Superposition Principle, we seek a particular solution y p = y p 1 y p 2 where y p 1 and y p 2 are particular solutions of y00 y0



Q Tbn And9gcqhxgrjwxzm1jyq Uidduyqfp07ryufflgr5gl6smrzc46lo9jz Usqp Cau



Q Tbn And9gcqqdjererih8cbajqv Puntih4ikbw7iy9bdv7cgyhxgixkwubp Usqp Cau
Q571 In Exercises 571–576 use variation of parameters to find a particular solution 1 y ″ 9y = tan3x 2 y ″ 4y = sin2xsec22x 3 y ″ − 3y ′ 2y = 4 1 e − x 4 y ″ − 2y ′ 2y = 3exsecx 5 y ″ − 2y ′ y = 14x3 / 2ex 6 y ″ − y = 4e − x 1 − e − 2xNeed to show that the denominator, x 1 3 e 3x 2 3, is never equal to zero One way to do this is by showing that the absolute minimum is this denominator is a positive number So the solution interval is (1;1) So, the nal solution is y = 1 x 1 3 e 3x 2 3 = 3 3x e3x 2;First Derivative dy/dx = 4x^3 6x 10 Second Derivative d2y/d2x = 12x^2 6 Method This process is called differentiation Consider x^4 With first differentiation this becomes 4x^3 With the second differentiation 4x^3 becomes (3x4) x^2 = 12x^2 if we have further differentiation 12x^2 => 24x;




Solucionarioecuacionesdiferencialesdenniszill7aedicion P
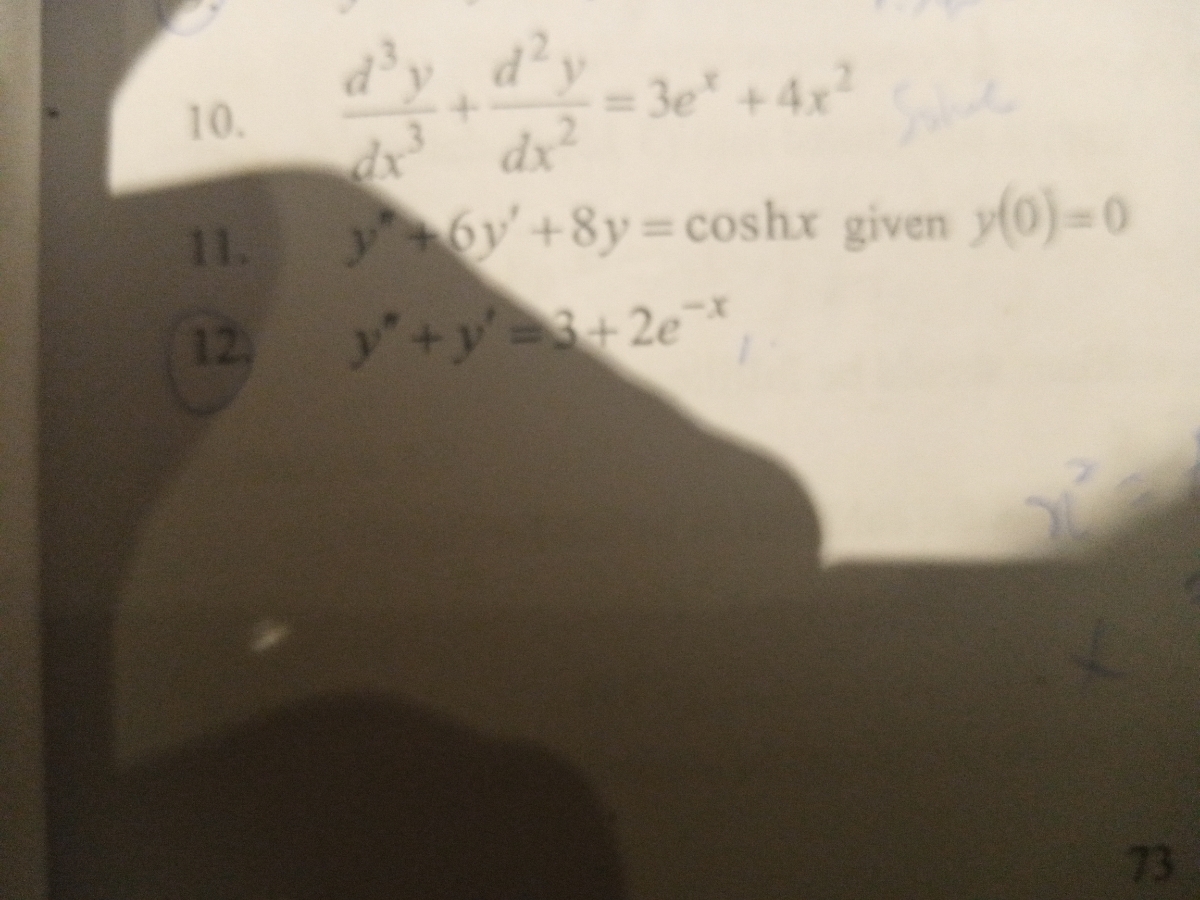



Answered 10 3e 4x Bartleby
Therefore the work done by the force field F(x,y) = (y2/x2) i−(2y/x) j in moving an object from P(1,1) to Q(4,−2) is Z C F·dr = Z C ∇f ·dr = f(4,−2)−f(1,1) = −1−(−1) = 0 9 Show that if the vector field F = P i Q j R k is conservative and P,Q,R have continuous firstorder partial derivatives, then ∂P ∂y = ∂Q ∂xExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sportsY2(x) = e−3x y2′(x) = −3e−3x y2′′(x) = 9e−3x Thus, y1 ′′ y1′ − 6y1 = 4e2x 2e2x − 6e2x = 4 2 −6e2x = 0 , and y2 ′′ y2′ − 6y2 = 9e3x − 3e3x − 6e3x = 9 −3−6e3x = 0 , verifying that e2x and e−3x are solutions to the given differential equation Also, it should
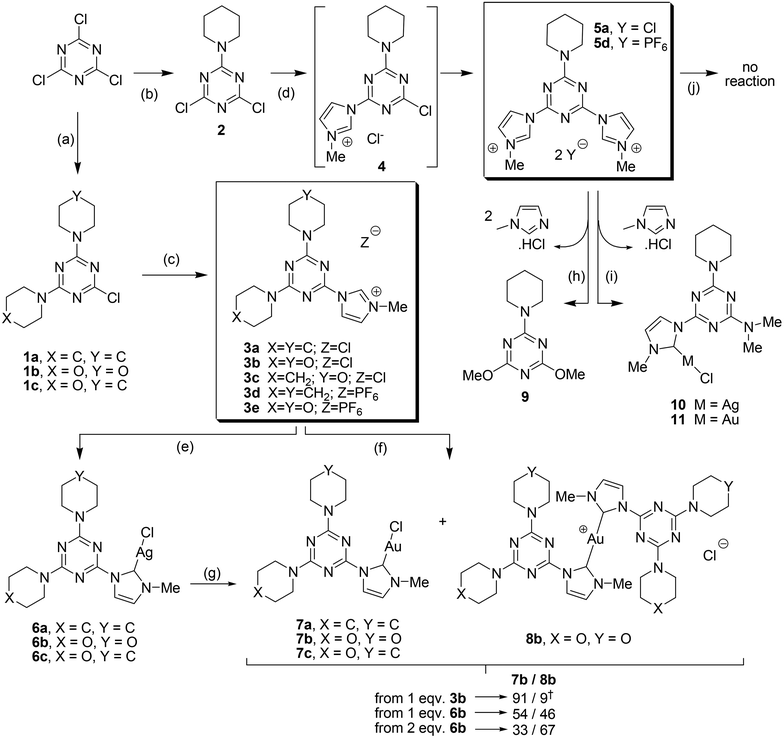



Convenient Syntheses Of Cyanuric Chloride Derived Nhc Ligands Their Ag I And Au I Complexes And Antimicrobial Activity Dalton Transactions Rsc Publishing Doi 10 1039 C3dte
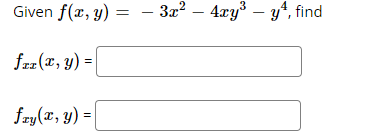



Answered Given F X Y 4xy Y Find Fzz T Bartleby
X = 4xy 2 So M y = N x and the given equation is exact Thus there is a function φ(x,y) such that φ x = M = 2xy2 2y andR φ y = N = 2x2y2x Integrating the first equation, we have φ(x,y) = (2xy2 2y)dx = x2y2 2xy h(y) Using φ y = N = 2x2y 2x, we have ∂(x2y22xyh(y)) ∂y = 2x2y 2x, 2x2y 2x h0(y) = 2x2y 2x, h0(y$=e^{\int 4/x \space dx}=e^{4\log x}=e^{\log \dfrac 1{x^4}}=\dfrac 1{x^4}$ Multiplying the given equation by $\dfrac 1{x^4}$ we get $\dfrac {xy^2e^{1/x^3}}{x^4}dx\dfrac {x^2y}{x^4}dy=0$ which is => x^2 4 y^2 4xy = 0 => x^2 4 xy 4 y^2 = 0 => (x 2y)^2 = 0 => x 2y = 0 => x = 2y => x/2 = y Now put the value of x/2 into (x y)/(x y) (x y) is (A) 2/3 (B) 2 3 (D) 10/3 (E) 4 spoiler?????/spoiler x^2 4 y^2 = 4 x y x^2 4 y^2 4 x y=0(it is in form a^22abb^2 where a=x and b=2y) so (x2y)^2=0 x=2y now actual




Solve Each Differential Equation Dy Dx 5y E 3x Chegg Com



2
Answer to 1 Find the equation of the tangent line to the curve x^2 4xy y^3 = 13 at the point (2,1) 2 Find the equation of the tangentC= 3Hence W(x) = 3e x2 Since W(0) 6= 0, we deduce that y 1;y 2 are independent solutions Therefore, the general solution is given by c 1y 1 c 2y 2 2 (T) Show that the set of solutions of the linear homogeneous equation ( ) is a real vector space Also show that the set of solutions of the linear nonhomogeneous equationFree separable differential equations calculator solve separable differential equations stepbystep



2



2
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorA) x2 y′′ 4xy′ 2 y =0 b) x2 y′′ 5 xy′ 4 y =0 c) 2 x2 y′′ 3xy′ 4 y =0 Solution a) Set y= xr we reach r (r − 1)4r 2=0 r1, 2 = −2, −1 (1) So the general solution is y= C1x− 2 C2 x− 1 (2) b) Set y= xr we get the indicial equation r (r − 1)5 r 4=0 r1, 2 = −2 (3) So the general solution is y= C1 x32 y'4xy=x^3 e^ {x^2}, y (0)=1 Ej 23 Parte 2 Explicación de la integral Ecuaciones lineales If playback doesn't begin shortly, try restarting your device



Http Tu Freiberg De Sites Default Files Media Fakultaet Fuer Mathematik Und Informatik Fakultaet 1 9277 Tochten Kl A Loesungen Pdf




A Reconsideration Of Jensen S Inequality And Its Applications Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub
3 Solution (ex siny 3y)0 y = e x cosy 3 ¡(3x¡ex siny)0 x = ¡3e x siny That is the differential equation is not exact 7 (yexy cos2x¡2exy sin2x2x)dx(xexy cos2x¡3)dy = 0Solution (yexy cos2x¡2exy sin2x2x)0y = e xy cos2xxyexy cos2x¡2xexy sin2x (xexy cos2x¡3)0x = e xy cos2xxyexy cos2x¡2xexy sin2x Thus, the differential equation is exact Then, Z (xexySolve the following system of equations 3x 4xy 2y = 2 3x 2y = 10 Solve the second equation for either of the unknowns I'll pick x 3x 2y = 10 add 2y to both sides 3x = 10 2y Divide both sides by 3 x = (10 2y)/3 factor out 2 x = 2 (5 y)/3 In the first original equation, 3x 4xy 2y = 2 substitute 2 (5 y)/3 for x 3 2Solve the Question We know that ( x − 2 y) ( x 2 y) = 4 and that ( x − 2 y) ( x 2 y) = x 2 − 4 y 2 Thus, Quantity A MUST be equal to 4, which is less than Quantity B The correct answer is B, Quantity B is greater



Solved Problems In Differential Equations 2500 Solved Problems In Differential Docsity




2xy 2 4 2 3 X 2 Y Y Y 1 8 F Y 8y Chegg Com
10Let X and Y be random variables with joint density function f (x, y) = 4xy 0 < x,y < 1 Find E(xy) 1 1 1 1 1 1 E(xy) = ∫ ∫ xy f(x,y) dx dy = ∫ ∫ xy 4xy dx dy = 4∫ ∫ x 2 y 2 dx dy = 4/9 0 0 0 0 0 0 11The joint pdf of two random variables X and Y is given by f(x,y) =See the answer See the answer See the answer done loading Show transcribed image text Expert Answer Who are the experts?



8izq2e00og1obm




Exam Solutions Of Introduction To Differential Equations Math 285 Docsity
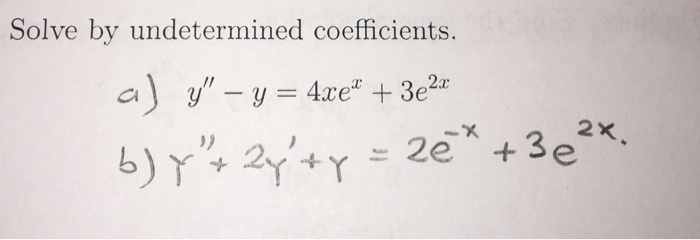



Solve By Undetermined Coefficients A Y Y Chegg Com



Www Math Kit Edu Iana3 Lehre Hm209s Media Hm2 07 Loe Pdf




Solve The Differential Equation I D 1 2 D Chegg Com




If Y 3e 2x 2e 3x Prove That D 2y Dx 2 5 Dy Dx 6y 0




What Is The Order Of The Differential Equation 1 Chegg Com
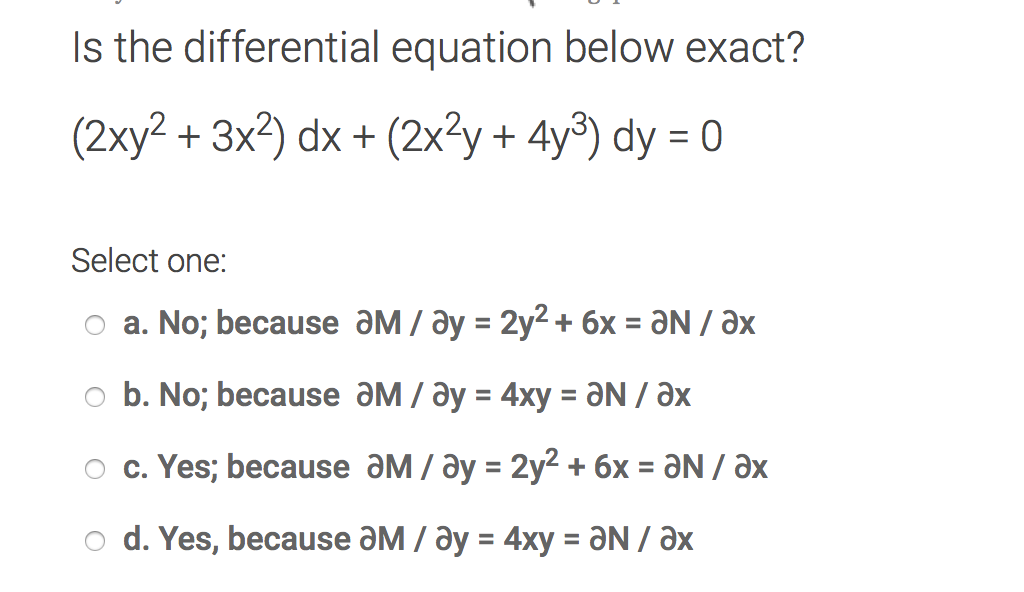



Is The Differential Equation Below Exact 2xy 2 Chegg Com



Y 4y X 2 2x What Is The General Solution Of Differantial Equation Quora




Solve The Following Differential Equations 1 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Youtube




How To Do Implicit Differentiation 7 Steps With Pictures



Link Springer Com Content Pdf 10 1007 2f978 3 662 053 9 9 Pdf



Web Iitd Ac In Dharmar Mal110 Mal110tutsheet5 Pdf




If 4 X 2 Y 128 And 3 3x 2y 9 Xy Then Find The Value Of X And Y Brainly In




Solutions To Midterm 1 Practice Problems




Elementary Differential Equation




Ross S L Introduction To Ordinary Differential Equations 4th Ed Wi




Y 3x Y 0 Find Two Power Series Solutions For This Linear De Based At The Ordinary Homeworklib



Solved Use Implicit Differentiation To Find Dy Dx If X 2 3e Y 2xy 2 Course Hero




Give The General Solution To X 2y 4xy 3e 3x Chegg Com




How To Do Implicit Differentiation 7 Steps With Pictures



Web Viu Ca Pughg Spring19 Math251s19n01 Math251s19n01t2sol Pdf




Solving Separable Differential Equations Calculus Socratic




Example 26 Find Particular Solution Log Dy Dx 3x 4y




1 Point If E X 1 And Var X 4 Then E 2 4x And Homeworklib




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Variation Of Parameters To Solve A Differential Equation Second Order Ex 2 Youtube




Differential Equations Pdf Free Download



Faculty Math Illinois Edu Ash De Desolschapter4 Pdf



2



Profs Info Uaic Ro Fliacob An2 17 18 Modelare matematica Resurse Patrick bourque Differential equations Pdf




Variation Of Parameters X 2y 3xy 4y X 2 Ln X Youtube



Numerical Solution For Generalized Nonlinear Fractional Integro Differential Equations With Linear Functional Arguments Using Chebyshev Series Advances In Difference Equations Full Text



The Solution Of Y 2x 2y E X Dx E X Y 3 Dy 0 If Y 0 1 Is Sarthaks Econnect Largest Online Education Community



2



2




Exact Equations Example 3 Video Khan Academy
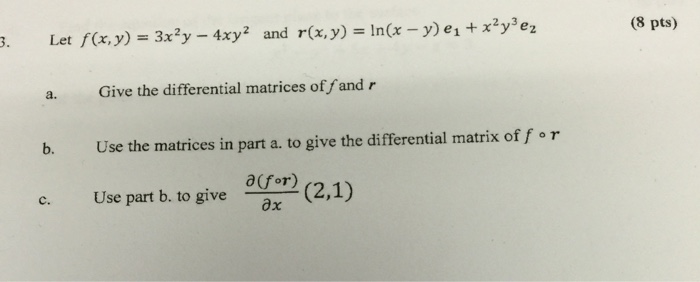



Let F X Y 3x 2y 4xy 2 And R X Y Ln X Chegg Com




Answered Y 4y 6e 3x 3e X Y 0 1 Bartleby



1



Www Math Upenn Edu Rimmer Math104 Newmaterialpracticebank Pdf



2




Solutions To Homework 2 Introduction To Differential Equations




Wolfram Alpha Examples Step By Step Solutions




Answered 2 For Which Of The Following Functions Bartleby




Example 2 Verify That Y E 3x Is A Solution Of Y Y 6y 0




Mudc



Arxiv Org Pdf 1908



Www Valpo Edu Student Asme Fe slides Math3slides Pdf




Xy Dy Dx Y 3e X 2 Youtube



Class 10 Rs Aggarwal Chapter 3e Cbse Solutions



Users Math Msu Edu Users Gnagy Teaching 12 Spring Mth235 L09 235 Pdf




Pdf Complete Solutions Differential Equations With Modeling Applications Differential Equations With Boundary Value Problems 5th Edition Juan Carlos Becerra Linares Academia Edu



Http Www Berkeleycitycollege Edu Wp Kpernell Files 16 05 Math3b Ch9 Practice Tst Pdf




Use A Graph Below Of F X 3e 9x 2 To Estimate The X Values Of Any Critical Points And Inflection Points Of F X Determine A Critical Points Enter As A Comma Separated List B Inflection P




Derivatives Days Ppt Download



Math Hawaii Edu Yuen 242handouts Math242 Chapters 16 17 Pdf



Http Tu Freiberg De Sites Default Files Media Fakultaet Fuer Mathematik Und Informatik Fakultaet 1 9277 Tochten Kl A Loesungen Pdf



Www Iitr Ac In Departments Ma Uploads Tute 21 Pdf




Engineering Mathematics Notes




3 Solve The Initial Value Problem A Y 2y Chegg Com



If Y E X What Is 2e 2x 3e X 2 Quora



Core Ac Uk Download Pdf Pdf
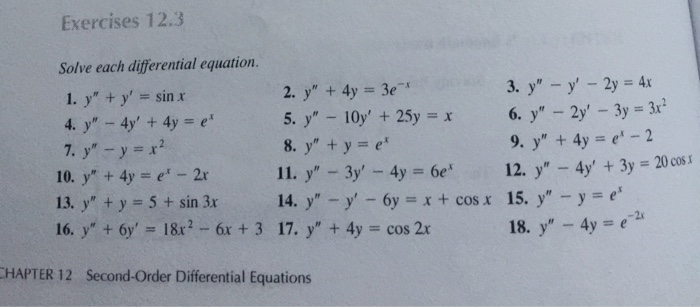



Exercises 12 3 Solve Each Differential Equation 1 Chegg Com




A Y X 3e X Mled Below Is Solution Of The Different Gauthmath



X 3e X 2 0 Dxの解き方を教えてください Yahoo 知恵袋
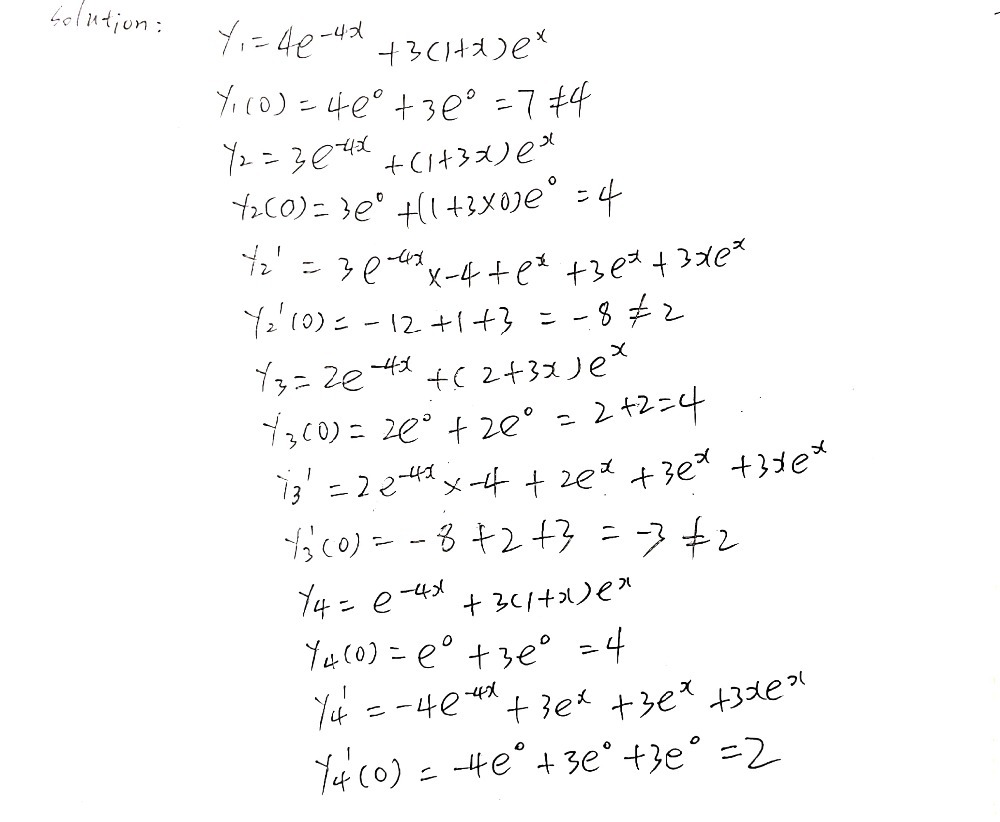



Which Of The Following Is The Particular Solution Gauthmath




Differential Equation Variation Of Parameters X 2y 4xy 6y X 4 Youtube
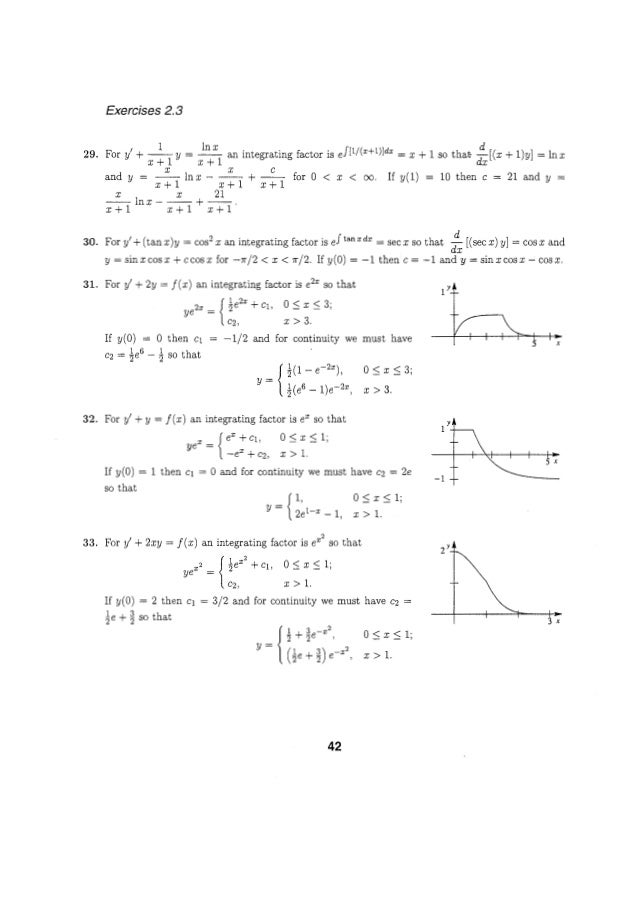



Solucionarioecuacionesdiferencialesdenniszill7aedicion P




How To Solve The Differential Equation X 2y 6xy 6y X 3 Logx Quora




Chapter 02 2500 Solved Problems In Differential Euations Docsity
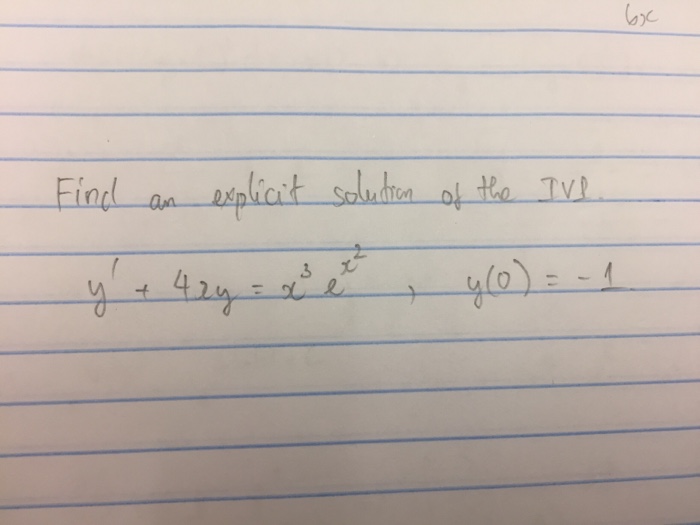



Find An Explicit Solution Of The Ivl Y 4xy X 3 Chegg Com



0 件のコメント:
コメントを投稿